általános relativitáselmélet
(gravitációs egyenlet, téregyenlet)
 A gravitáció
csaknem teljesen Einstein által kidolgozott
(1915) egyik elmélete.
A gravitáció
csaknem teljesen Einstein által kidolgozott
(1915) egyik elmélete.
Newton gravitációs elméleténél általánosabb,
a gyenge gravitációra, ill. a kis sebességek
tartományában azonban határesetként visszaadja a Newton-törvényt.
Newtonnak a gravitációs
mező révén nagy távolságban is azonnal érvényesülő erőhatásról
alkotott elképzelését a tömeg által eltorzított
téridő koncepciójával helyettesítette.
A Föld pl. a Nap
nagy tömege által eltorzított téridő
miatt kering a Nap körül.
A téridő torzulását a következő analógiával
szemléltethetjük: képzeljünk el egy gumilepedőt,
amelyet egy nehéz golyó (a "Nap")
egy bemélyedéssel eltorzít; a körülötte keringő kisebb golyó (egy "bolygó")
a bemélyedés felé fog tartani, s így a nagy golyó látszólag vonzza a kicsit.
Az általános relativitáselméletet a fénysugaraknak a Napközeli
elhajlására (a képen) és a Merkúr
pályájának precessziójára vonatkozó tapasztalatok
kísérletileg is alátámasztják.
Az elmélet egyéb következményeiként a fekete
lyukak létét és a világegyetem
tágulását említhetjük.
Az általános relativitáselmélet Riemann
terekben dolgozik.
Egy tér metrikáját a metrikus tenzor (gmn)
határozza meg. A metrikus tenzorból vezethetők le a tér "görbeségére"
vonatkozó mennyiségek. Az elmélet lényegében a tömeg térbeli eloszlásának metrikus
tenzorra gyakorolt hatását mutatja meg:
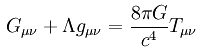 ahol
ahol
Gmn az Einstein
tenzor
L a kozmológiai állandó
Tmn pedig az energia-impulzus
tenzor
Einsteinnek ezt az egyenletét gravitációs (vagy tér-) egyenletnek nevezik.
Gyenge terek esetében ez az egyenlet visszavezethető a Newton-féle gravitációs
törvényre.
Felhasznált irodalom
 A gravitáció
csaknem teljesen Einstein által kidolgozott
(1915) egyik elmélete.
A gravitáció
csaknem teljesen Einstein által kidolgozott
(1915) egyik elmélete.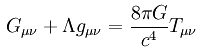 ahol
ahol