kvantummechanika
(kvantumfizika)

A mechanika atomi nagyságú, 10^-10 m vagy még kisebb távolságokra alkalmazható változata, amely lehetőséget ad a molekulák és az atomi szinten ismert valamennyi jelenség leírására.

A kvantummechanika szinonimájaként gyakran használják a kvantumfizika és kvantumelmélet kifejezéseket, de ebbe időnként beleértik a kvantummechanika előtti régebbi kvantumelméleteket is.

A kvantummechanika fontos műszaki alkalmazásai közé tartoznak a szupravezetők, a lézer és az elektronikai eszközök.
1900-ban, a feketetest-sugárzás (azaz a testek hőmérsékleti [elektromágneses] sugárzásának) vizsgálata Max Planck német fizikust arra a következtetésre vezette, hogy a sugárzás elemi energiacsomagokból (fotonokból) áll, amelyek energiája E = hv, ahol h a Planck-állandó, v pedig a sugárzás frekvenciája.
Az 1905-ben felfedezett fényelektromos jelenség és az 1923-ban felismert Compton-effektus további bizonyítékokkal szolgált arra, hogy a kisugárzás kis adagokban (kvantumokban) történik.
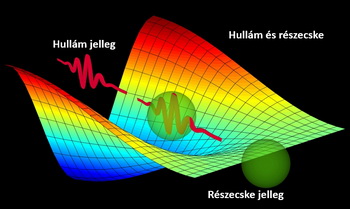
A hullámnak elgondolt fény ilyenformán részecskeszerű viselkedést mutatott.
1923-ban Louis de Broglie francia fizikus arra jutott, hogy az anyagi részecskék, viszont hullámszerű tulajdonságúak. Feltevése szerint az elektronhoz vagy más részecskékhez l = h/p hullámhosszú hullám kapcsolható, ahol p a részecske impulzusa.
Az elektronok hullámtermészetének végleges bizonyítékát 1927-ben Clinton Davisson (1881-1958) és Lester Germer (1896-1971) amerikai fizikusok adták meg az elektronok kristályrácson való elhajlásának megfigyelésével.
1926-ban Erwin Schrödinger osztrák fizikus matematikai kifejezést állított fel az anyagok hullámtermészetére. A hidrogénatomra felírt Schrödinger-féle egyenlet szerinti színképvonalak jól egyeznek a ténylegesen megfigyeltekkel.
A Schrödinger-féle kvantummechanikai módszerekhez hasonlót (de nehezebben felfoghatót) dolgozott ki Werner Heisenberg 1925-ben.
A kvantummechanika további fontos eleme a Heisenberg-féle határozatlansági reláció (1927) és a Pauli-féle kizárási elv (1925) is.
A nagy sebességű részecskék leírására alkalmas kvantummechanikai elméletet, a relativisztikus kvantummechanikát Paul Dirac angol fizikus fejlesztette ki 1928-ban.
A kvantummechanika szigorú, formális matematikai felépítésében, mely többek közt Paul Dirac és Neumann János nevéhez fűződik, a kvantummechanikai rendszerek lehetséges állapotait egységvektorokkal ("állapotvektorok") reprezentálják, melyek a komplex szeparábilis Hilbert-tér egységgömbjét alkotják (az "állapotteret").
A kvantumtérelmélet végleges kidolgozása a 40-es évekre tehető, amikor megalkották a részecskekeletkezéssel és -megsemmisüléssel foglalkozó kvantumelméletet. Az elektronok és más egyszerű vagy összetettebb kvantumrendszerek hullámtulajdonságait hullámfüggvények segítségével írják le. A hullámfüggvények viselkedését a Schrödinger-egyenlet határozza meg. A részecskék (pl. az elektronok) a kvantummechanikában már nem tekinthetők pontszerűnek, hanem a hullámfüggvények által meghatározott módon szétterülnek. A hullámfüggvény abszolút értékének négyzete megadja egy adott pontban tartózkodásuk valószínűségét. A kvantummechanika szükségképpen valószínűségi leírást ad a jelenségekről, a klasszikus mechanikával ellentétben, ahol a testek adatai (legalábbis elméletben) pontosan kiszámíthatók.
A kvantummechanikában a viselkedést jellemző értékek diszkrétek is lehetnek, pl. az atombeli elektronok energiája nem vehet fel folytonos értékeket, hanem csak bizonyos meghatározott, elkülönülő értékeket: ahogyan mondani szokás, az energia kvantált. Ha egy gerjesztett atom elektronja egy bizonyos energiaszintről egy kisebb energiájú szintre lép, fénykvantum bocsátódik ki.
A kvantumállapotok mérésekor a diszkrét értékek valamelyikét kapjuk eredményül, a hullámfüggvény által meghatározott valószínűséggel.

Felhasznált irodalom