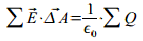
Maxwell-egyenletek
(Maxwell-törvények)

Maxwell (1831-1879) skót elméleti fizikus 1864-ben írta le az elektromágneses mezőt leíró, azok kölcsönhatásait bemutató egyenleteit, melyek nagyon fontos következményekkel jártak és megoldották a fény természetéről folytatott évszázados vitákat.
Az egyenletek egyenes következményének tekinthető a töltésmegmaradás elve, és a fény hullámtermészetének pontos leírása.
Az egyenletek (törvények) sorrendje egyes szakirodalmakban eltérő.

Maxwell I. egyenlete / törvénye (Gauss tétele)
Akárhogyan veszünk fel a térben egy zárt felületet, a ki- és belépő erővonalak számának különbsége mindenkor a felület által körülvett elektromos töltések algebrai összegének 1/e₀-szorosát adja:

Ahol:
e - a közeg elektromos permittivitása
E - az elektromos térerősség
Q - az elektromos töltés
A - a felület

Maxwell II. egyenlete / törvénye (Faraday indukciós törvénye)
Időben változó mágneses fluxust körülölelő bármely zárt görbére az elektromos mező örvényerőssége:

Ahol:
E - az elektromos térerősség
f - a mágneses fluxus
t - az idő
l - a vezető hossza

Maxwell III. egyenlete / törvénye (Gauss mágneses törvénye)
A mágneses mező forrásmentes (nincsenek mágneses töltések), vagyis bármely zárt felületen áthaladó teljes mágneses indukciófluxus zérus, azaz bármely térrész mágneses forráserőssége nulla:

Ahol:
A - a felület
B - a mágneses indukció

Maxwell IV. egyenlete / törvénye (Ampére-féle gerjesztési törvény)
Az elektromos mező időbeli változása örvényes mágneses mezőt kelt:

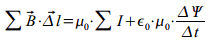
ahol az eltolási áram

Felhasznált irodalom